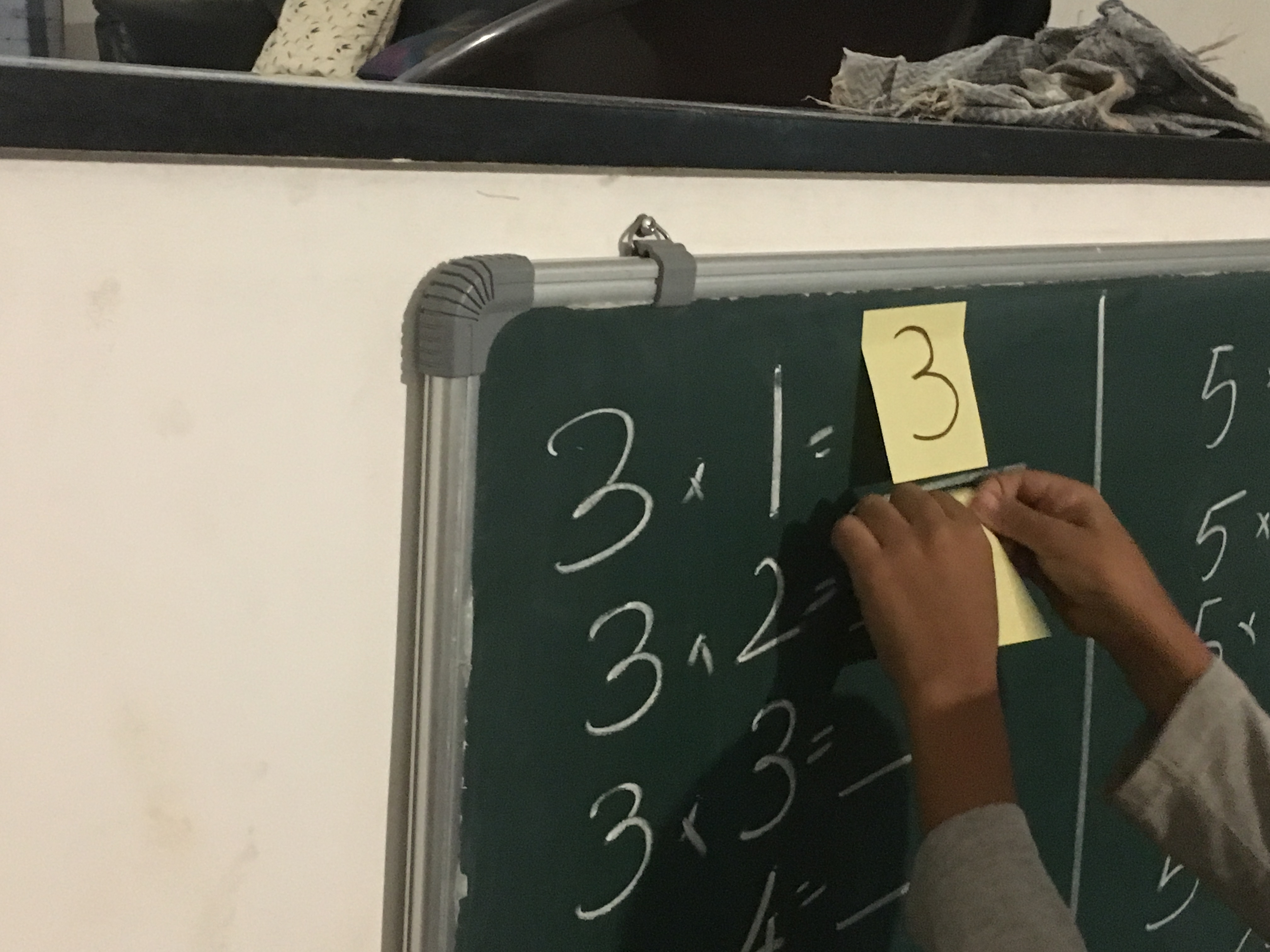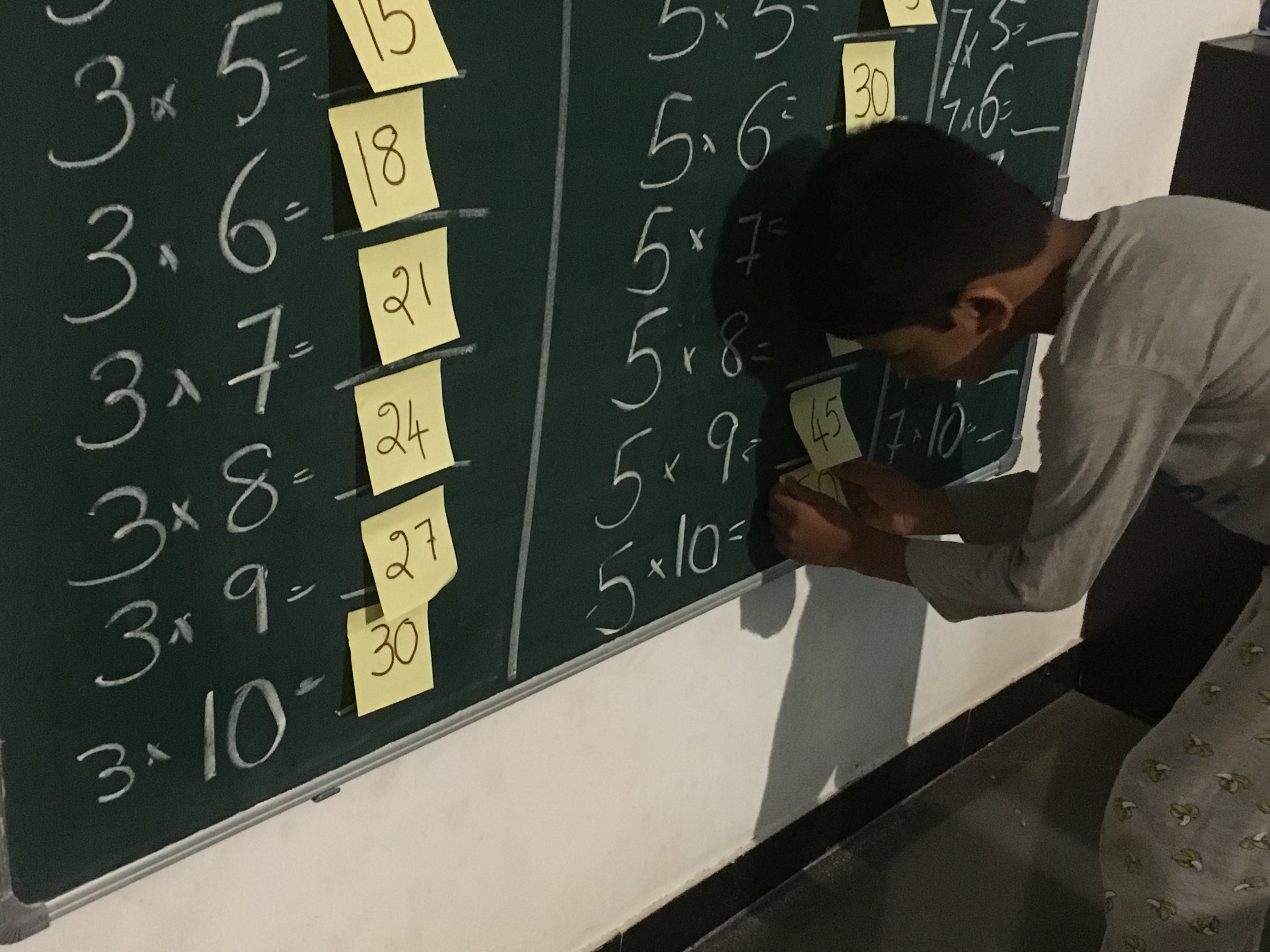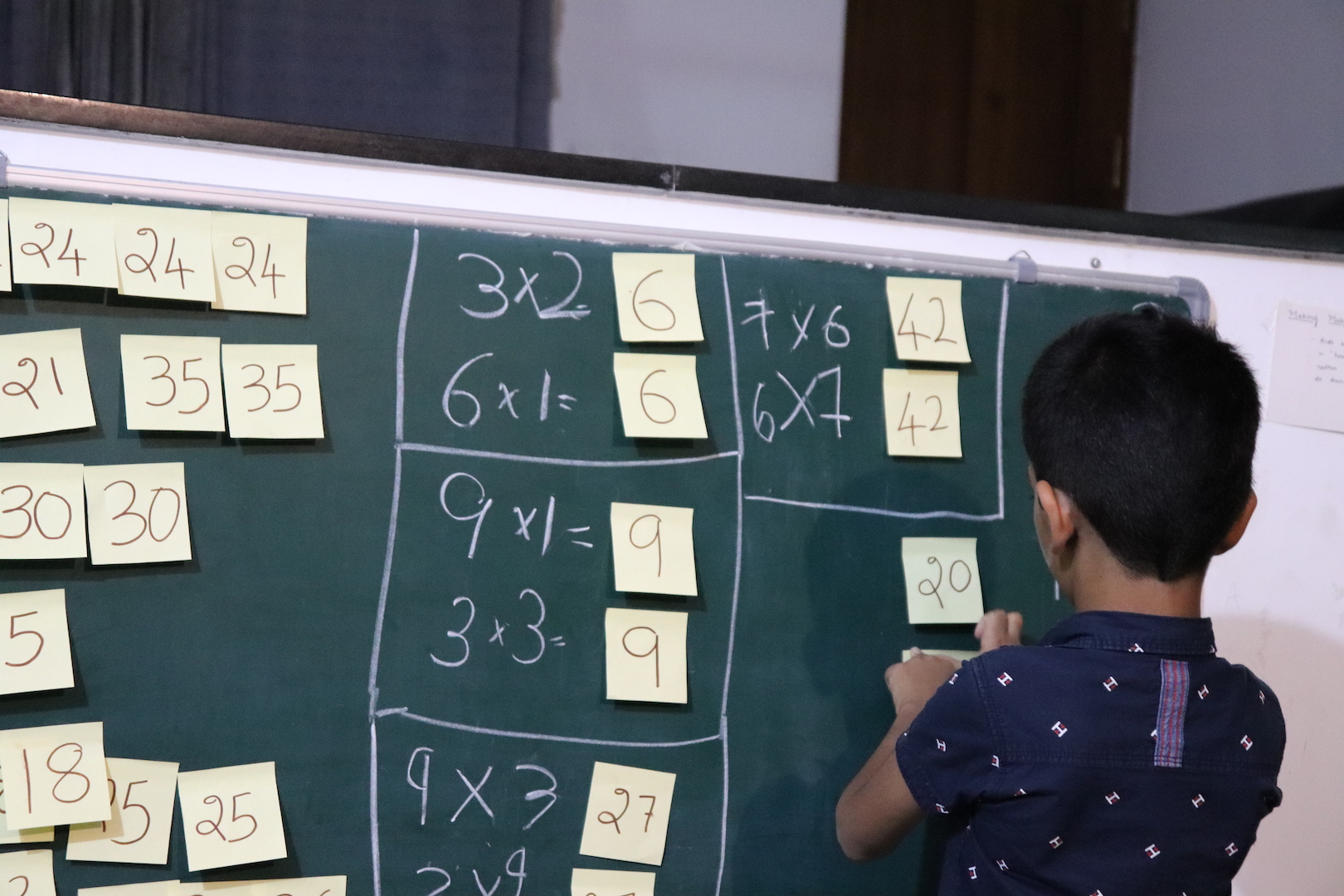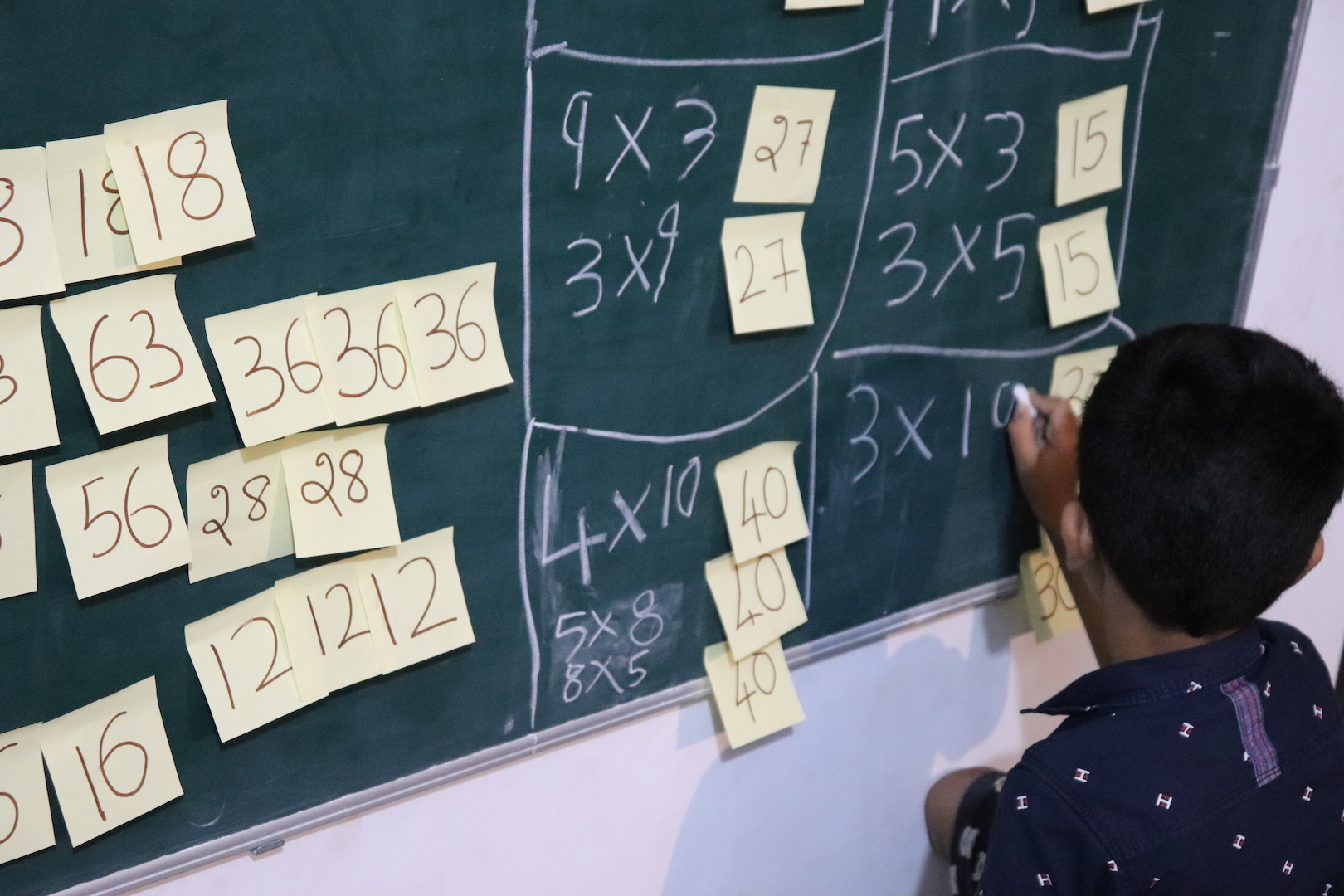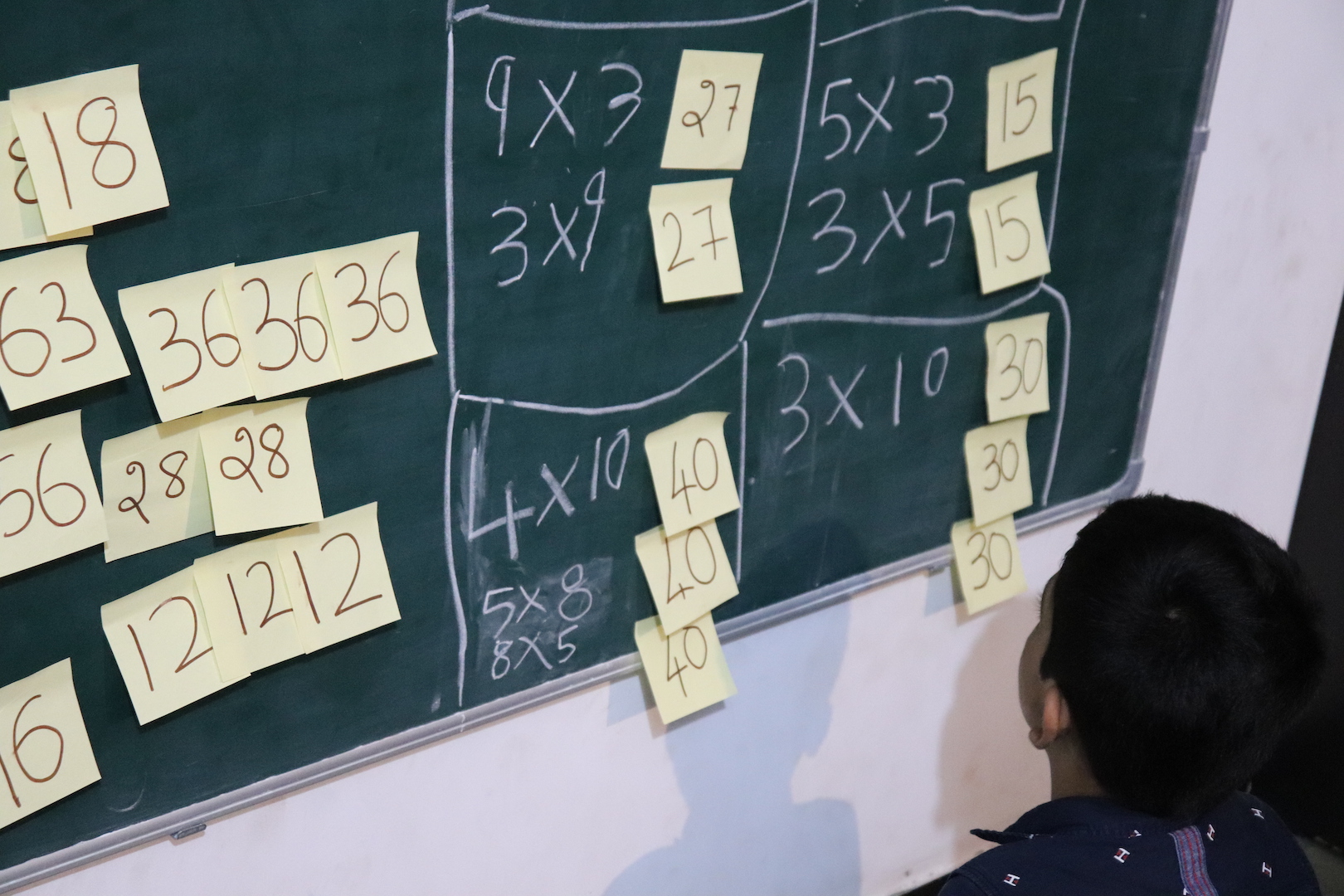The word “multiplication tables” brings back memories of only one thing from my childhood – “mugging”. As a child I simply had to learn multiplication tables. I couldn’t ask for a reason why. My parents would explain to me the benefits of learning tables by-heart. They would even give me sufficient time to learn it. Figure out ways to learn it. But when the exam time came, I better have learned it by-heart already. There was no way around it. My school, the neighbourhood with other kids everybody basically reinforced the need-to-learn-multiplication-tables-by-heart ™. So I would spend days and months learning it by-heart.
One onezaar one One twozaar two ..... ..... ..... Eight onezaar eight Eight twozaar sixteen Eight threezaar twenty-four .... .... .....
“I was mostly in college when I realised that it is not “eight eightzaar sixty-four”. It actually is “eight eights are sixty four.” I never bothered to question “zaar” as a child. Because questioning anything was a big big big big risk. What if my questions pissed off my teachers?”
As a kid, I did not like it at all. Now as an adult I know that multiplication tables are useful. Although I hardly use tables beyond 10 for mental math. Calculators are always around so performing multiplication is not an issue.
My son turned 8 this year. If he was in a regular school, he would be in 3rd standard. Many of his friends in the neighbourhood are ramping up on math-tables. So Advay would come home asking about it and slightly wanting to learn it.
Nandini & I tried the standard way to get him to learn tables. Advay did not like that approach. He continued to enjoy multiplying each time and writing the answer rather than just memorising it. For him – “multiplication must be performed, not memorised.” We had to come up with a reason, a purpose for having him memorise math tables. So, we came up with one idea.
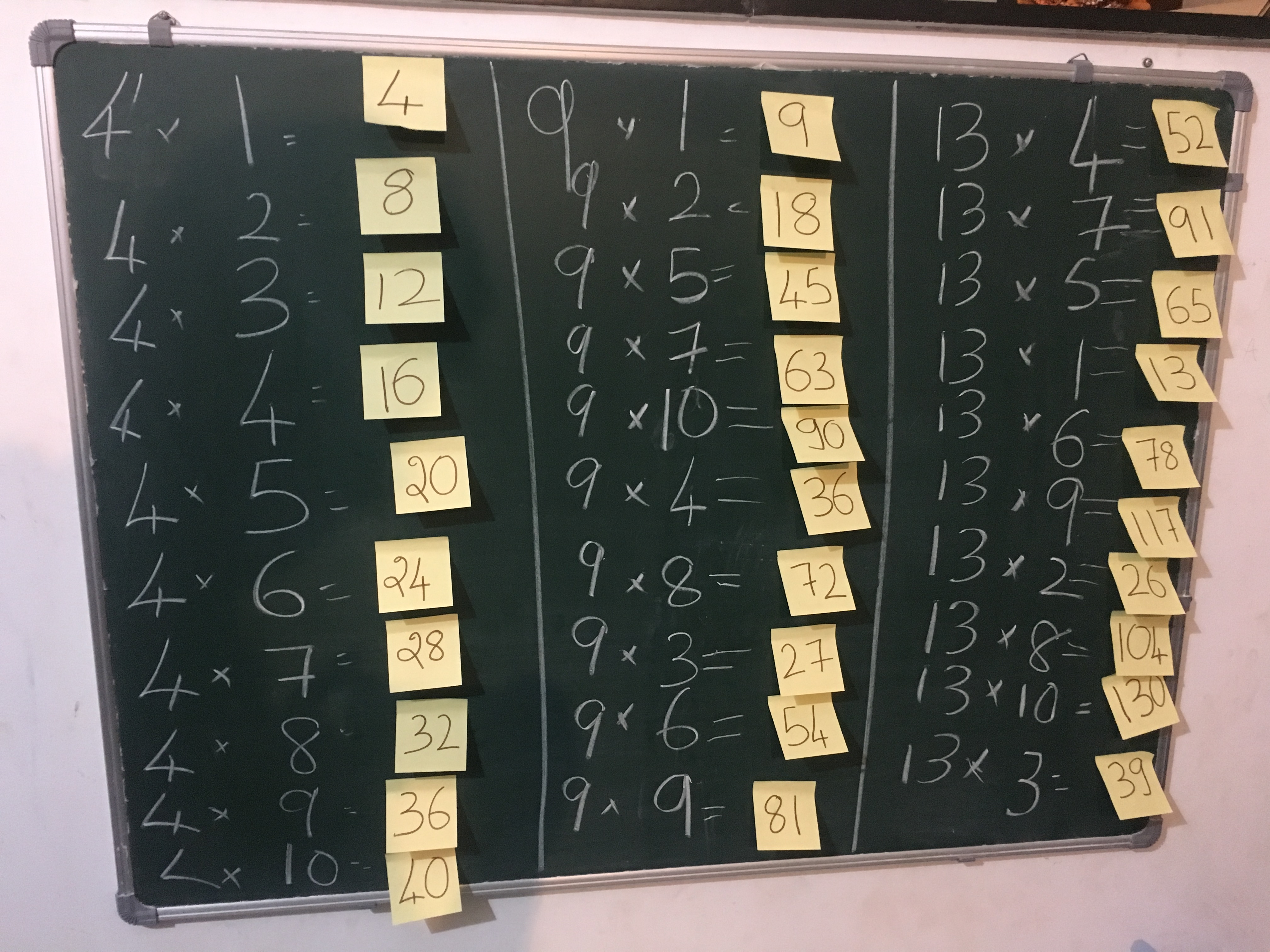
I setup a puzzle for him at home. All over the house, I put up post-it-notes with numbers that show up in the math-tables for 3, 5 & 7. The post-it-notes were pasted on doors, window frames, switch boards, desks, chairs tub-seats, kitchen racks, washing machine, fridge etc. I then put up a fill in the blanks on the green board at home.
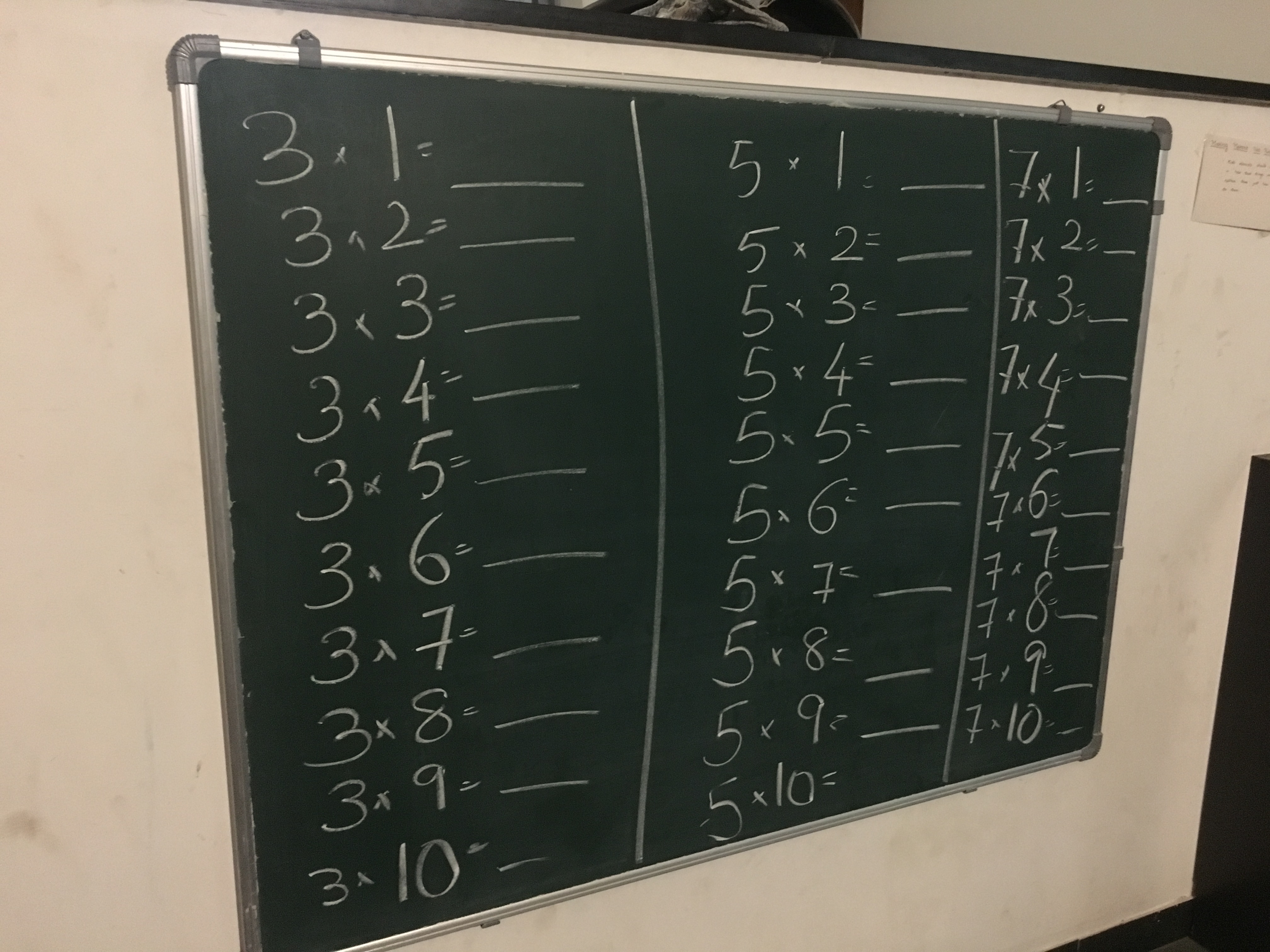
With this, I setup a treasure hunt game for him. The game was to go around, pick up post-it-notes and paste them next to the appropriate place on the green board. Advay simply loved the idea.
He ran around the house and harvested the post-it-notes and properly pasted them next to the numbers. He simply loved the whole game.
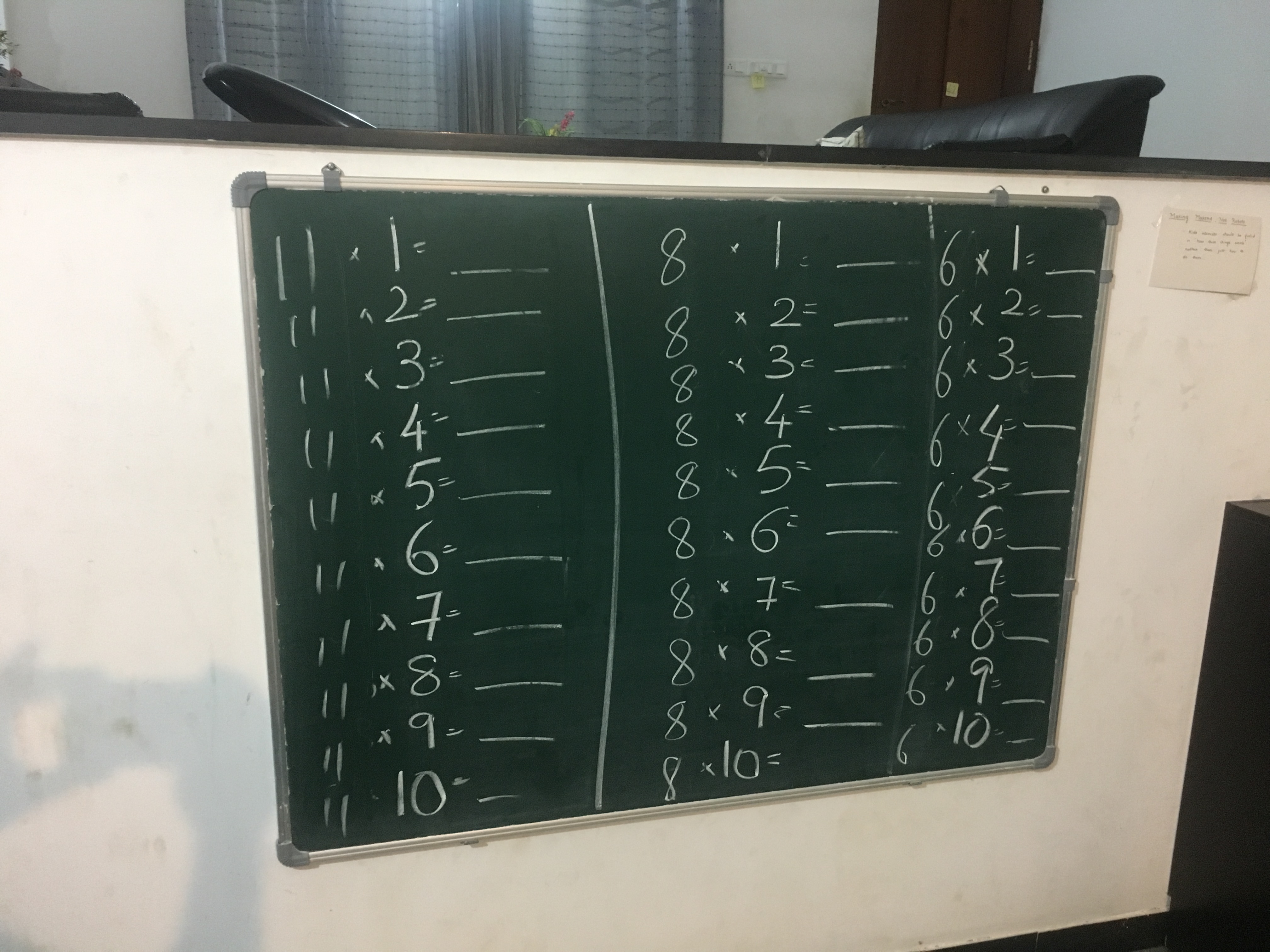
While he was able to quickly “hunt” for numbers against 3 and 5 tables, he was a bit slow with 7 tables. We told him – “Ok, tomorrow we will setup treasure hunt for 6, 8 & 11. If you memorise them before the game begins, you will be able to finish it quickly.”
Suddenly, it seemed like Advay found his purpose to memorise the tables. But he still did not want to give up his “multiplication must be performed, not memorised” motto. So he sat with Nandini and worked out the math tables for 6, 8 & 11. They worked out the answers, ways to memorise them and also the reason for memorising them. He was able to recall 11 tables easily, because he identified a pattern. 6 & 8 was a bit of struggle. While he did commit the tables to memory, he did not do it by “mugging”. The tables meant logic, math and pattern to him. It was not abstract sounds like “eight eightzaar sixty-four.”
It appeared like he had made some progress. The time to test came. I setup the board for home once again. This time Nandini suggested Advay to not pick post-it-notes in sequence, but to pick them as and when he found it and paste them against the right place on the board.
Whenever he found numbers that he couldn’t immediately figure out its place for on the board, he pasted them temporarily on the chair in front of the board. And they would eventually go up on the board.
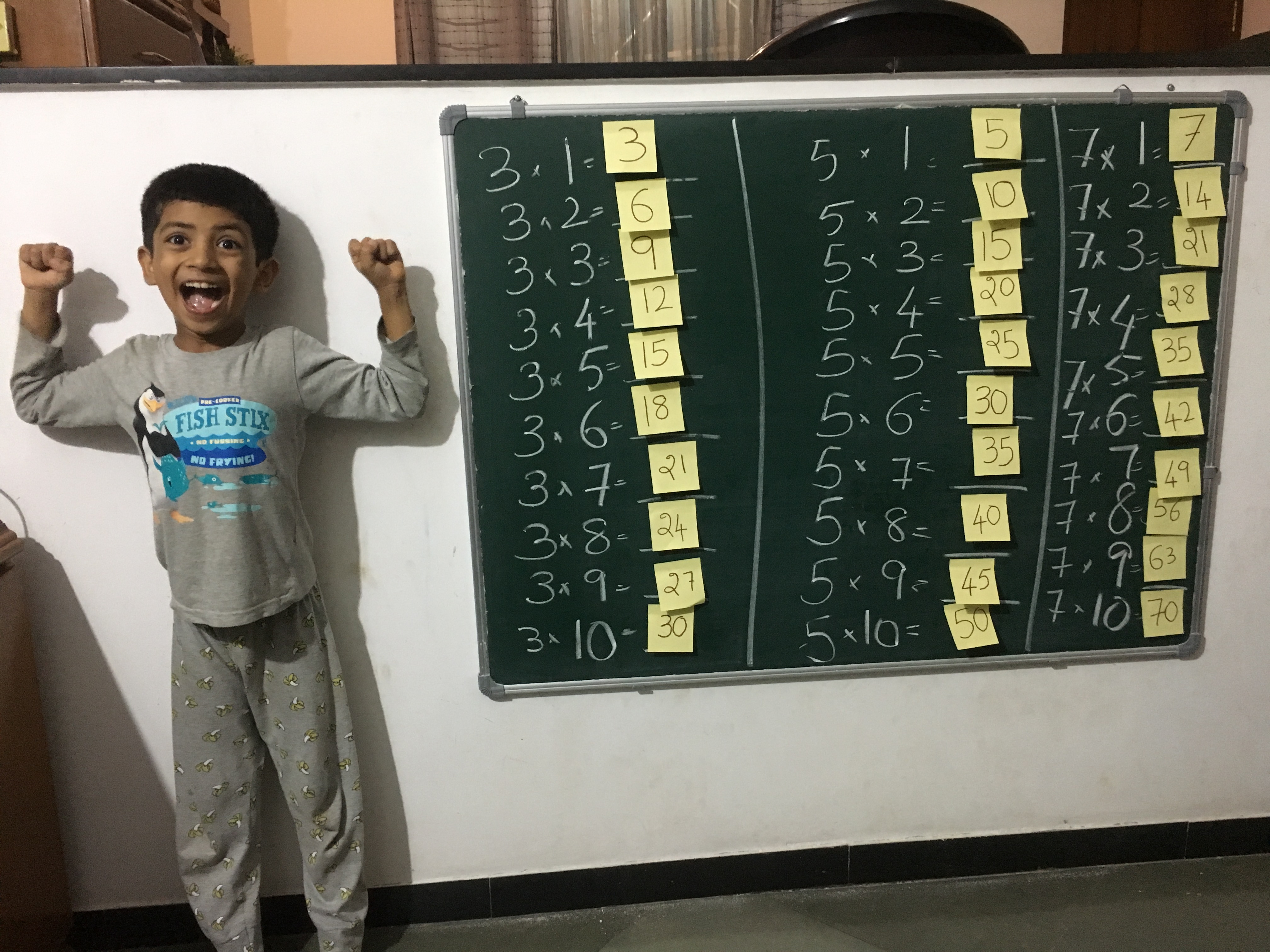
Finally he was done with the tables.
He seems to enjoy playing this game a lot. He keeps asking me to set it up for him every evening. Due to work, I was unable to set it up for him for a few days. And I started to notice how much he was missing playing it.
Yesterday, I setup treasure hunting game for 4, 9 & 13. But this time, I did not give him fill in the blanks in sequence. Some of them were in random order. But he still managed to complete the treasure-hunt-puzzle properly.
The last two times he played this game, he noticed something interesting. He said – “Appa, some numbers show up in many tables, right?”
Now that we have 90 post it notes with numbers for 3, 4, 5, 6, 7, 8, 9, 11 & 13 tables; we began observing patterns.
- Why does 30 show up in 3, 5 and 6 tables?
- How come many numbers from 3 tables also show up in 6 and 9 tables?
- Oh, 3×5 and 5×3 are the same?
- How come 3, 7, 11 & 13 shows up only once?
I asked Advay to paste all post-it-notes in a collage on the board.

Next, I told him to arrange numbers such that all 24s went into one group, all 35s into one group and so on.

From the board I then asked him to take away notes that had numbers showing up only once. A lot of clutter disappeared from the board.

Then I explained to him that 6 is both 3×2 and 6×1. And that 9 is both 3×3 and 9×1. The idea was to figure out the tables in which a post-it-note-number would show up among the tables we played a puzzle game (which was: 3, 4, 5, 6, 7, 8, 9, 11 & 13). So, even though 6 is 2×3, we won’t write that on the board because we never played treasure-hunting game for 2 tables.

After solving for numbers 6 and 9, I placed two 27s below it and asked Advay to figure out the tables in which 27 would show up. He got it and started writing out the answer.
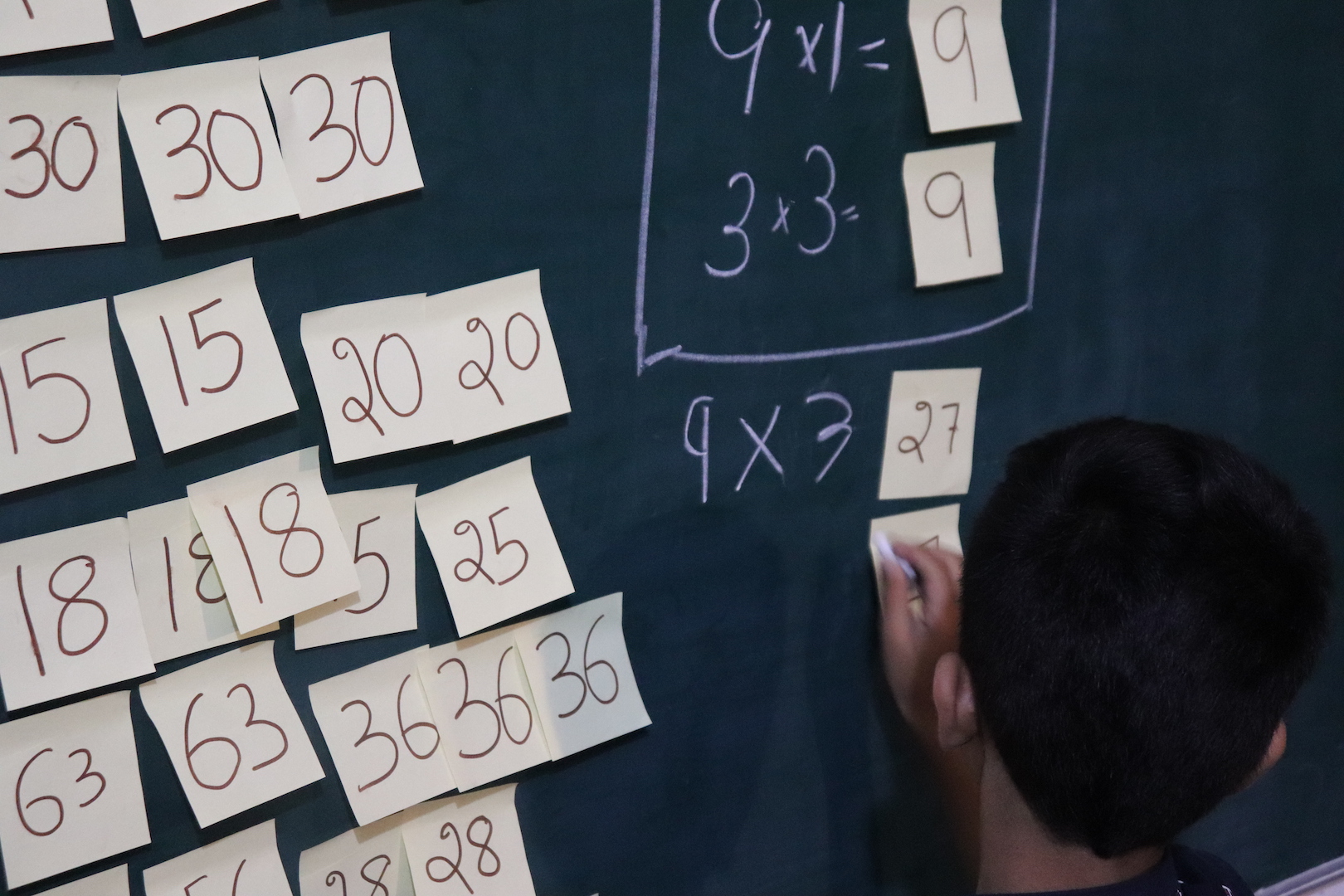
And slowly, he figured it out for all notes.
Finally it was all done.
While playing the game he figured that if AxB is C, then BxA is also C. For many numbers he seemed to intuitively know which tables they are likely to show up in.
Let’s talk about results: Has he become perfect in math tables? Not yet. He has gotten better for sure. But more importantly, he has genuinely begun to enjoy multiplication in general & learning the tables in particular. To Nandini & me: that counts!